About Kinematic Couplings

Kinematic couplings (KC's) are precision-machined mechanical contacts used to precisely locate components with respect to each other. Traditional KC's place a triangular arrangement of three hemispheres on one component into three corresponding 'vee-grooves' on a mating component, deterministically constraining all six degrees of freedom of motion. Given deterministic locating, analytical relations give the contact forces, contact stresses, and contact deflections for a given coupling geometry.

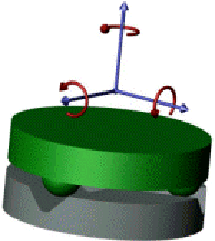
Traditional coupling model

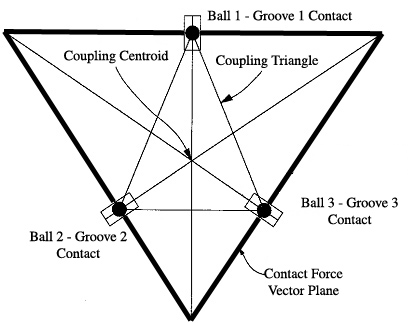
Triangular layout diagram

In recent years, PERG researchers have developed new types of KC's tailored to various applications, including:

• Automotive engine manufacturing, for which 'quasi-kinematic couplings' enable extremely precise and repeatable location of components in progressive stations of a machining line.
• Sheet metal stamping, for which kinematic 'Flex Vees' combine die-set bushings, posts, and springs into two simple elements, possibly enabling die changes in seconds.
• Semiconductor manufacturing, for which a pattern of three two-way slots can locate a thin sheet of silicon precisely and accurately.
• Generic high-load applications, for which Canoe Ball couplings mimic the contact surface of a large sphere and are highly repeatable (~10 microns) under traditionally extreme stresses.

It is envisioned that couplings can be developed for numerous other applications. Specifically, project work began in September 2000 to develop standard KC interfaces linked to open-architecture information technology (IT) applications to enable quick-change modularity of industrial robots and robot subassemblies. This project is supported by ABB, Ford, Polaroid, and Teradyne; for a detailed description of work, visit the Case Studies section of the website.

For more detailed information about KC's, see:

• Introductory notes on KC's and Hertz Stress Contact Design.
• A Microsoft Excel spreadsheet for designing kinematic couplings.
• Additional references, including links to several of Prof. Slocum's patents for kinematic coupling designs.
• More detailed information about each of the different coupling types:
  1. Pin Joints
  2. Elastic Averaging Techniques
  3. Planar Kinematic
  4. Quasi-Kinematic
  5. Kinematic

For more information on the general design process, please see the following selected lectures from Prof. Slocum's Design and Manufacturing I Course at MIT (2.007):

• Lecture 1: The Design Process
• Lecture 2: Fundamentals
• Lecture 3: Deterministic Design

And one set of lecture notes from Prof. Slocum's Precision Machine Design Course at MIT (2.75):

• Topic 4: Error in Precision Machines

Home | About KC's | Design Process | Documents | Tools | Case Studies | References